Skewness And Kurtosis Spss

Just like skewness kurtosis is a moment based measure and it is a central standardized moment. But if you have just a sample you need the sample skewness. You can also see that spss has calculated the mean 46 93 metres and the standard deviation 21 122 metres.

contoh teks plakat ucapan terima kasih contoh polisi keselamatan dan kesihatan pekerjaan contoh syarikat multinasional di malaysia contoh set induksi yang menarik contoh surat wasiat tanah di malaysia corak bingkai tulisan khat contoh surat pengesahan pendapatan tidak bekerja contoh ulasan penilaian prestasi kerja

Normality Skewness And Kurtosis Youtube

Descriptive Statistics Spss Annotated Output

How To Calculate Skewness And Kurtosis In Spss Quick Spss Tutorial

Skewness Spss Part 1 Youtube

Skewness Quick Introduction Examples Formulas

Frm part 1 statistics.

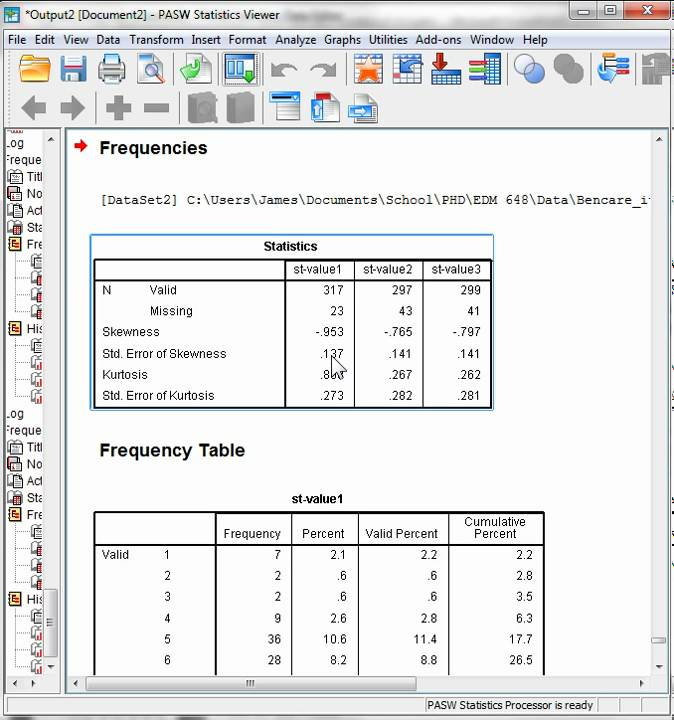
Skewness and kurtosis spss. Notice how much different the results are when the sample size is small compared to the true skewness and kurtosis for the 5 000 results. For a sample size of 25 the skewness was 356 compared to the true value of 0 007 while the kurtosis was 0 025. You should now be able to calculate statistics for skewness and kurtosis in spss. Population or just a sample.

Okay that s it for this quick tutorial. N represents the number of observations. Kurtosis is sensitive to departures from normality on the tails. If you have the whole population then g1 above is the measure of skewness.

When both skewness and kurtosis are zero a situation that researchers are very unlikely to ever encounter the pattern of responses is considered a normal distribution. This lesson is part 2 of 3 in the course basic statistics frm. It indicates the extent to which the values of the variable fall above or below the mean and manifests itself as a fat tail. Comparing measures of sample skewness and kurtosis.

Kurtosis is a measure of whether the distribution is too peaked a very narrow distribution with most of the responses in the center hair et al 2017 p. Peak is higher and sharper than mesokurtic which means that data are heavy tailed or profusion of outliers. For skewness if the value is greater than 1 0 the distribution is right skewed. The same is true of skewness.

Distribution is longer tails are fatter. Leptokurtic kurtosis 3. Interpretation of skewness kurtosis coskewness cokurtosis. Outliers stretch the horizontal axis of the histogram graph which makes the bulk of the data appear in a narrow skinny vertical range thereby giving the skinniness of a leptokurtic distribution.

Because of the 4th power smaller values of centralized values y i µ in the above equation are greatly de emphasized. Because it is the fourth moment kurtosis is always positive. The outliers in a sample therefore have even more effect on the kurtosis than they do on the skewness and in a symmetric distribution both tails increase the kurtosis unlike skewness where they offset each other. In spss the skewness and kurtosis statistic values should be less than 1 0 to be considered normal.

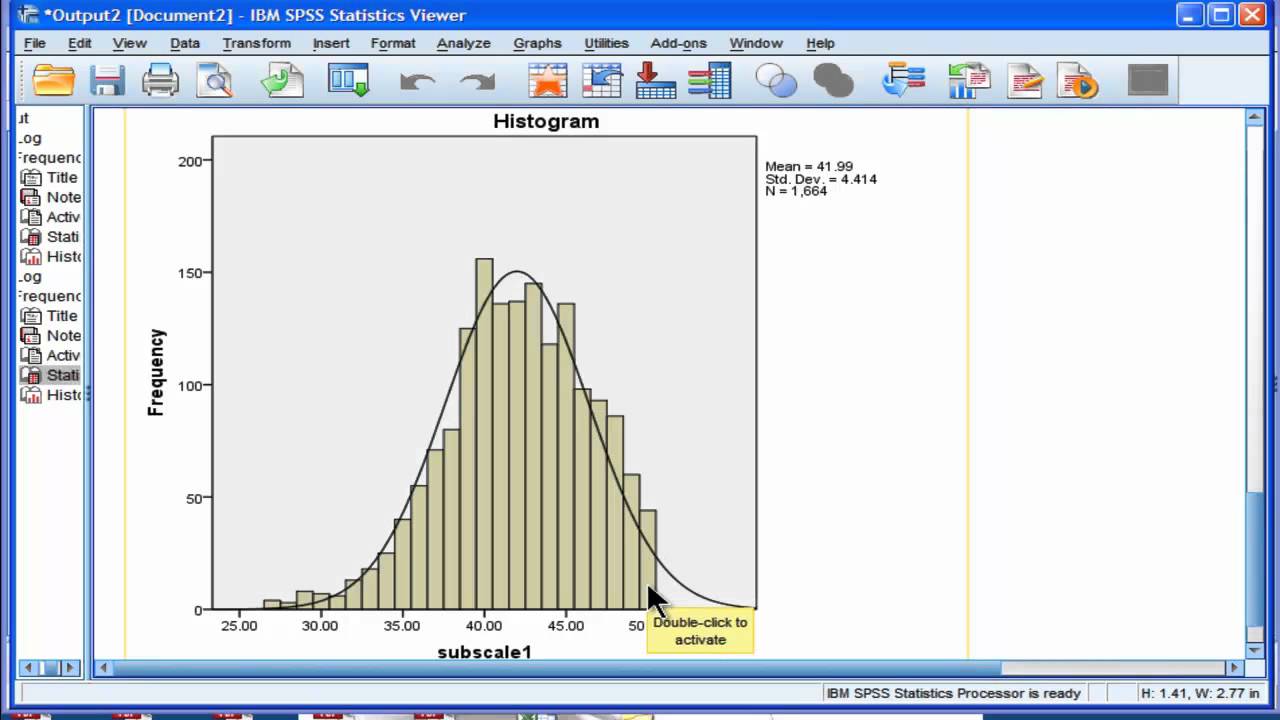
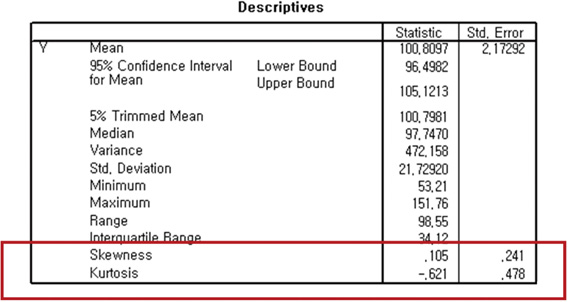
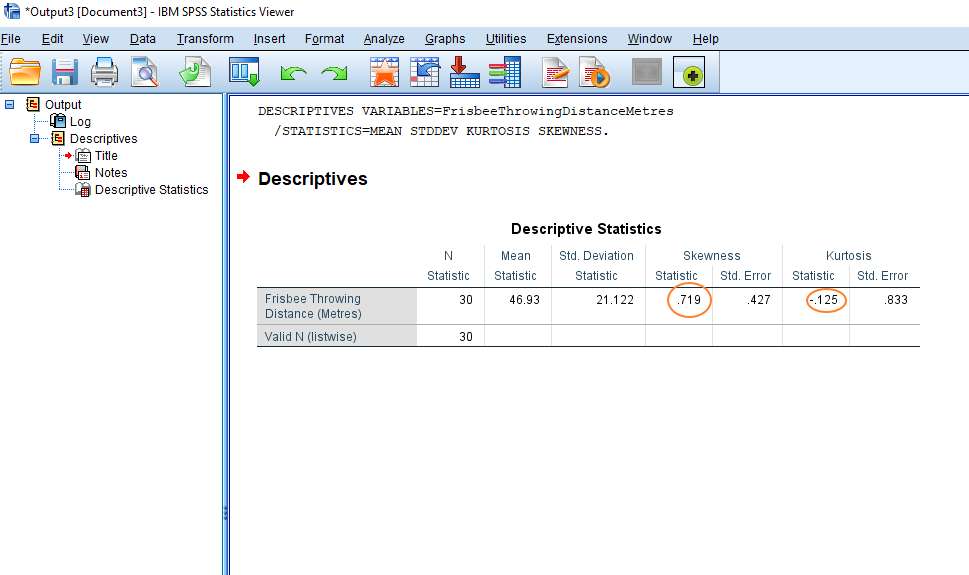
In this video i show you very briefly how to check the normality skewness and kurtosis of your variables. The skewness statistic is 719 and kurtosis is 125 see above. As skewness involves the third moment of the distribution kurtosis involves the fourth moment.